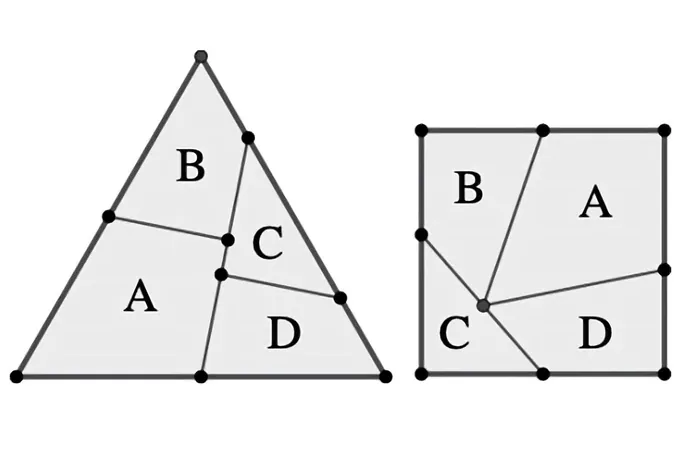
Un mystère mathématique vieux de plus d'un siècle vient de trouver une réponse concluante ! Les mathématiciens d'une équipe internationale ont prouvé que la méthode proposée par Henry Dudeney en 1907, consistant à transformer un triangle équilatéral en un carré grâce à des découpages et réarrangements, est la plus efficace possible. Ce type de problème, connu sous le nom de dissection géométrique, fascine tant les amateurs de puzzles que les chercheurs.

La solution originelle nécessitait quatre pièces, et jusqu'à récemment, personne n'avait pu prouver qu'une solution plus efficace était impossible. C'est maintenant chose faite ! L'étude, récemment publiée sur arXiv, a démontré que quatre pièces étaient bel et bien le minimum nécessaire. Grâce à une méthode innovante, les chercheurs ont utilisé des diagrammes de correspondance pour examiner les relations entre les bords et les sommets des pièces découpées, apportant ainsi une nouvelle dynamique à l’analyse de ces configurations.

L’équipe a d’abord éliminé l'idée qu’une solution à deux pièces fût possible, puis a soigneusement exploré toutes les configurations envisageables avec trois pièces. Leur constat est sans appel : aucune configuration à trois pièces ne mène à un carré parfait. Cette avancée représente un tournant significatif dans notre compréhension des défis posés par les dissections géométriques.

Cette recherche va bien au-delà de la simple curiosité mathématique. Ses applications s'étendent à divers domaines comme la conception textile, le développement de matériaux, et même des applications dans l'art numérique. La méthode mise au point par cette équipe pourrait également faciliter la résolution d'autres problèmes complexes de dissection, non encore résolus.

Les diagrammes de correspondance se sont révélés être des outils précieux, car ils permettent de visualiser les contraintes géométriques imposées par les pièces découpées. Ce sont des éléments graphiques qui offrent une perspective temporelle sur les problématiques qui préoccupent les mathématiciens depuis des siècles.

Enfin, cette découverte marquante souligne non seulement une étape importante dans l'histoire des mathématiques, mais pose également les fondements pour des recherches futures. Les scientifiques envisagent sérieusement d'adapter cette approche à d'autres formes géométriques, promettant ainsi de nouvelles percées dans ce champ d'étude fascinant.

Saviez-vous que la dissection géométrique a été un sujet d'intérêt depuis l'Antiquité ? Il s'agit non seulement d'un exercice intellectuel, mais aussi d'outils pratiques pour optimiser des processus de production. De plus, ces techniques sont aujourd'hui mises à profit dans des domaines tels que l'architecture, la robotique et même l’architecture logicielle.

Que pensez-vous de cette percée incroyable en géométrie ? Restez connecté pour découvrir les prochaines innovations dans ce domaine passionnant !