Introduction

In a significant scientific breakthrough, a team of researchers has successfully calculated the Jones polynomial through innovative quantum simulations of braided Majorana zero modes (MZMs). Their groundbreaking study, recently published in *Physical Review Letters*, reveals how they achieved this feat by simulating braiding operations of Majorana fermions, which are seen as key players in the realm of quantum computing and topological quantum states.

The Importance of the Jones Polynomial

The Jones polynomial is a fundamental link invariant that helps determine the topological equivalence of two knots, making it a valuable tool across multiple fields, including DNA biology, molecular synthesis, and condensed matter physics. However, calculating the Jones polynomial is notoriously challenging, as it lies within the #P-hard complexity class. Traditional classical algorithms struggle with this task, requiring exponentially more resources, which makes the researchers' quantum approach all the more exciting.

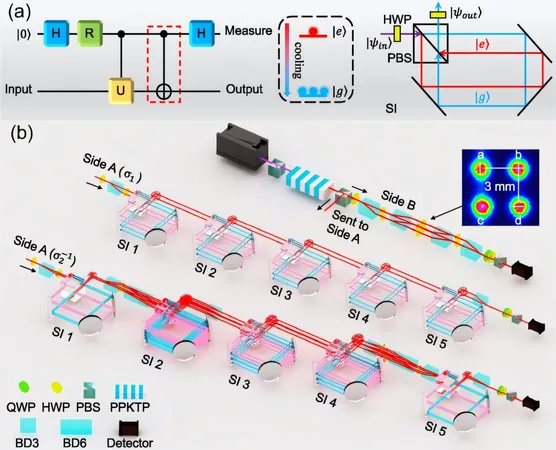
Quantum Simulations and MZMs

Utilizing a sophisticated photonic quantum simulator, the team employed two-photon correlations and nondissipative imaginary-time evolution. They executed a variety of MZM braiding operations that produced anyonic worldlines across multiple links, conducting a series of experimental studies to explore the topological properties of non-Abelian anyons.

Technical Achievements

In particular, the researchers effectively simulated the exchange operations involving a single Majorana zero mode from a Kitaev chain, detected the non-Abelian geometric phase in a more complex two-Kitaev chain setup, and even delved into higher-dimensional studies involving semion zeroth modes. Their braiding processes demonstrated remarkable resilience to local noise, highlighting their robust approach to maintaining quantum resources.

Enhancements in Experimental Design

A significant enhancement in their technique was the transition from a single-photon encoding method to dual-photon spatial methods. This alteration allowed for a dramatic increase in the number of quantum states that could be encoded using coincidence counting of two photons, showcasing an advancement in their experimental design.

Innovative Cooling Device

Moreover, the team introduced an innovative Sagnac interferometer-based quantum cooling device, facilitating the transformation of dissipative evolution into nondissipative evolution. This advancement not only recycled photonic resources but also enhanced the simulator's capability, contributing to more complex, multi-step quantum operations.

Results and Implications

Remarkably, the research team demonstrated a high fidelity in their experimental setup, achieving an average fidelity of over 97% for the quantum states and braiding operations. They successfully simulated various braiding operations across three Kitaev chain models, resulting in the calculation of Jones polynomials for five distinct topological knots, effectively distinguishing between topologically inequivalent links.

Conclusion

This pioneering work in topological quantum computing holds promise for further advancements in statistical physics and could lead to improved technologies in areas such as integrated DNA replication and molecular synthesis. As the field of quantum computing rapidly evolves, these advancements drive us closer to realizing the full potential of quantum information technologies. This research not only marks a significant achievement in mathematical physics but could pave the way for future applications that could revolutionize scientific understanding as we know it!