Quantum walks are revolutionizing the landscape of computing by leveraging the enigmatic principles of quantum mechanics such as superposition, interference, and entanglement to unlock computational power far surpassing that of traditional methods. Recently, a cutting-edge research team at the National Innovation Institute of Defense Technology within the Academy of Military Sciences in China has published a groundbreaking review, delving into the mechanics, applications, and hurdles of quantum walks and quantum walk computing. This comprehensive review was featured on November 13 in "Intelligent Computing".

As the quantum counterparts of classical random walks, quantum walks utilize the peculiarities of quantum phenomena to construct advanced algorithms aimed at solving various complex problems, including database searches, network analysis, and quantum simulations. The realm of quantum walks encompasses several types, such as discrete-time, continuous-time, discontinuous, and nonunitary quantum walks. Each type boasts distinct advantages that enhance computational capabilities.

Discrete-time and Continuous-time Quantum Walks Explained:

1. **Discrete-time quantum walks** function through a series of transitions that occur sequentially, using coin-based models like Hadamard and Grover walks, or coinless models such as Szegedy and staggered quantum walks to navigate graph structures. Conversely, **continuous-time quantum walks** run on graphs employing time-independent Hamiltonians, which makes them exceptionally efficient for spatial exploration and problem-solving.

2. The combination of the two types leads to **discontinuous quantum walks**, merging strengths from both models, facilitating universal computation through seamless state transfers. Meanwhile, **nonunitary quantum walks** involve open quantum systems like stochastic and open quantum walks, serving vital roles in simulating processes such as photosynthesis and intricate quantum Markov behaviors.

The intriguing interplay between discrete and continuous quantum walks allows for faster diffusion rates compared to classical random walk models while exhibiting strikingly similar probability distributions. It’s noteworthy that with the versatility of these models, various discrete formulations can adapt based on specific graph structures.

Advantages and Applications:

The authors of the review highlight that quantum walks not only offer evolutionary advantages but also significantly enhance sampling efficiency and tackle computational challenges that were previously deemed insurmountable by classical systems. The breadth of physical quantum systems utilized in implementing quantum walks showcases the immense potential within both discrete and continuous models, leading to quantum walk-based algorithms.

There are primarily two strategies for implementing quantum walks in practice:

- **Analog Physical Simulation** employs solid-state, optical, and photonic systems to actualize specific Hamiltonians directly, promoting scalability but lacking in error correction measures—pressing concerns when simulating expansive graphs.

- **Digital Physical Simulation** constructs quantum circuits aimed at mimicking quantum walks, complete with error correction, albeit facing challenges in circuit efficiency. Nevertheless, digital implementations promise quantum speedups and versatility across diverse graph structures.

Key Areas of Application:

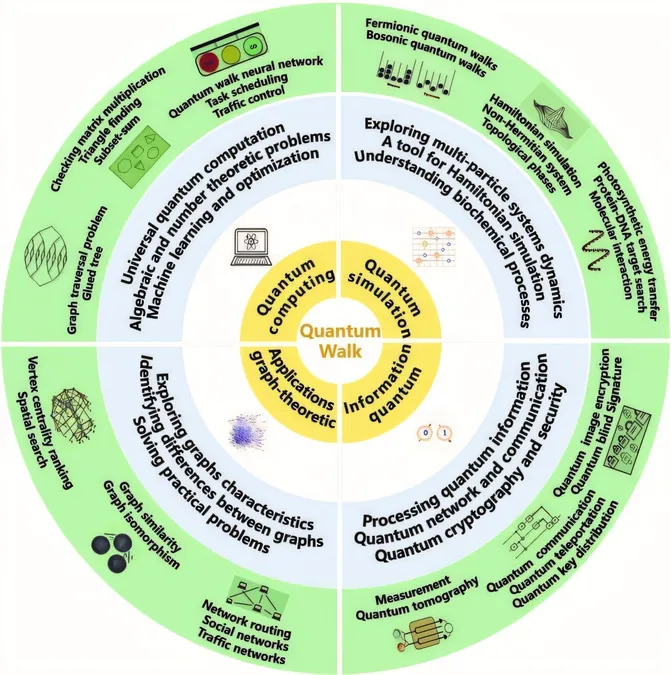
Quantum walks find applications in four main sectors:

1. **Quantum Computing**: Presenting pathways for universal quantum computation and expediting solutions in algebraic and number-theoretic problems, with growing potential in machine learning and optimization fields.

2. **Quantum Simulation**: Crucial in replicating uncontrollable quantum system behaviors, these walks offer insights into complex phenomena that defy classical analysis, applicable to multi-particle systems and biochemical modeling.

3. **Quantum Information Processing**: Essential for managing quantum states—from preparation and manipulation to characterization and transmission—quantum walks also bolster quantum cryptography and security solutions.

4. **Graph-Theoretic Applications**: Their association with graph structures yields promising innovations for resolving graph-related challenges, analyzing characteristics, and gauging vertex centrality.

The Road Ahead: Challenges and Innovations

Despite the swift advancements in quantum walk computing, notable hurdles remain. These include the development of effective algorithms, scaling up physical implementations, and the challenge of integrating error correction or fault tolerance in quantum walks. However, these challenges illuminate potential avenues for future breakthroughs and cutting-edge developments in the field of quantum science.

As we stand on the brink of this quantum revolution, the implications of quantum walk computing could redefine the computational landscape, offering unprecedented solutions to challenges across various scientific realms. Keep an eye out as this technology evolves—it may well lead us to a future we can only dream of today!